 |
| |
A Colorful Journey through Endless Patterns of Quick Wits |
|
|
|
|
|
|
|
|
|
Home /
Puzzles /
Put-Together Puzzles /
The Tangramion |
|
|
|
|
|
|
|
|
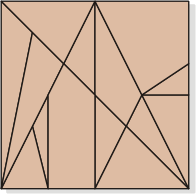
This is a new assembling puzzle consisting of seven
two-sided tiles which initially form a perfect square as
that shown at left. Using all the seven tiles, you can
solve different challenges both entertaining and
cognitive. Some of them are posed
below:
1. Form different shapes shown below with all seven tiles each
time*.
2. What's the ratio of all the seven tiles of the Tangramion?
3. A square can be formed in several different ways. Can you find
all of them?
4. What's a total number of convex shapes which can be formed,
using all the seven tiles each time?
Note, that tiles can be rotated and flipped over, but
not overlapped. |
|
|
|
|
|

|
Assemble these shapes, using
all the seven tiles of the Tangramion.
|
|
|
|
|
|
|
|
The Tangramion Background |
This new assembling or put-together
puzzle has been devised as a result of a thorough
analysis of two classic puzzles --
Archimedes' Square Stomachion2 and the
T. A. Snider Diamond Puzzle.
|
 |
Archimedes' Square Stomachion. |
|
|
 |
Diagram of the T. A. Snider Diamond Puzzle. |
|
|
|
|
|
The first puzzle has a long
history, and is, in fact, the oldest known puzzle of
this type, and, perhaps, the oldest puzzle ever
confirmed in a written document. It's attributed to
Archimedes, and has more than 22-century history. Its
ancient origin has been proved after amazing
modern investigations of the
Archimedes Palimpsest, a 174-page
volume, created a thousand years ago, then lost and
found and again lost, until it was finally rediscovered
in the last decade of the 20th century. Then it was
carefully restored and exactly translated. One of the
Archimedes Palimpsest's parts describes The Stomachion
or Loculus of Archimedes (Archimedes' Box).3
Archimedes' puzzle contains 14 different tiles, and it
might seem that such a puzzle set proposes very wide and
varied possibilities for creative puzzle play. But, in
fact, numerous and mostly inconvenient tiles make it
somewhat complicated creating and solving challenges and
having natural fun with this very old and famous puzzle.
And this is what makes Archimedes' Square Stomachion
rather a
math object than a really fun puzzle.
There were some attempts to reduce the total number of
tiles so that to add more fun to the puzzle, and at the
same time not to lost its original taste and save as
much as possible of its properties. One of these
attempts was resulted with
11 tiles, again giving very
nice math puzzle, but still not too much adding puzzling
fun to it.
One day, comparing Archimedes' Square Stomachion (a) and
the T. A. Snyder Diamond Puzzle (b) I've discovered that
surprisingly many dividing lines of their grids exactly
match, and pro tanto many tiles are exactly the same.
|
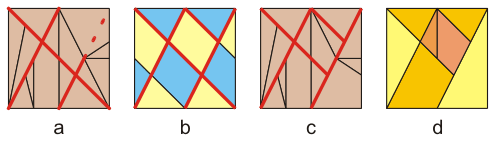 |
|
|
Compared diagrams: From
Archimedes' Stomachion and the Diamond Puzzle to the
Tangramion.
|
Moreover, if in the traditional
drawing of Archimedes' Square Stomachion we exchange two
blocks of tiles as shown (c), we can easily spot even
more of the same elements in the puzzles what is very
thrilling if to take into consideration the fact that both of
them use a very unusual pattern of their grids. In
particular, the Diamond Puzzle has a rare grid with the
combination of its diagonals running at 45 and 26,565...
degrees almost not used in other Tangram-like puzzles.
And the very same degrees for main diagonals of its grid
are used in Archimedes' Square Stomachion.
In the third diagram (c) the main dividing lines (shown
in red) isolate six clearly visible regions exactly
coinciding with regions of the Diamond Puzzle and
containing from one to four original tiles of
Archimedes' Square Stomachion. Now it's pretty easy to
spot the most natural way how to merge some of the
original tiles so that to reach the goal of reducing the
number of pieces and making them more convenient, and as
a result, to make the puzzle more playable and fun.
Additionally, having 14 tiles in Archimedes' Square
Stomachion and keeping in mind "standard" 7 tiles in the
traditional Tangram, the very pleasant possibility of
getting the very same number of tiles in our new puzzle
was quite appealing. And so, adding a short vertical
line to the whole red pattern (c), finally we have our
set of tiles (d). By the way, you can notice that the
tiles form the 7 shape in the middle of the square (d).
Lastly, combining two puzzle names, Stomachion and
Tangram, we got the name for this new puzzle, Tangramion.
|
|
|
|
 |
Printable Puzzle: To
solve the challenges of the Tangramion you can print its
tiles. For this, click the image marked with the "pp"
pictogram (as that shown at left) to go to a new window
with the puzzle tiles; then you can print them and cut
them out. |
|
 |
PDF Version: Also,
you can download a PDF file of the puzzle, and then
print it out if you wish. For this, use the link marked
with the "pdf" pictogram (as that shown at left). |
|
 |
Copyright Note: Note
that the entire puzzle and its challenges are copyrighted, so
you can print them for your own use only, and not for
any kind of commercial profit.
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
Last
Updated: April 6, 2012
Posted: October 26, 2007 |
|
|
|
|
|
|
|
|
|
