 |
|
|
|
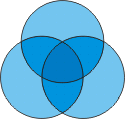
Three circles can form
seven non-overlapping arco-triangles. |
|
|
|
|
If you take three circles and
overlap them as shown in the diagram at right, you can
see that the whole shape is divided into seven
non-overlapping arco-triangles. An arco-triangle is a
shape formed with three arcs which are crossing in three
vertices of the arco-triangle.
Using four and five circles we can form shapes divided
into 11 and 16 non-overlapping arco-triangles,
respectively. Can you find those shapes? Note that
circles can be of any necessary sizes. Also, within a
shape you can have some other, non-triangular shapes
which can be ignored.
Some questions.
1. Can you improve the above results?
2. What are the maximal results for six and more
circles?
3. What are the maximal results if each resulting shape
does not contain free, non-triangular space(s)? This
means that the shape, in fact, should consist just of
non-overlapping arco-triangles like that formed of three
circles; see above right diagram.
Write
us if you can improve the above results or will find
maximal solutions for six and more circles. |
|
